GPN CTF 2025: "variants"

index

Hello!

In this brief write-up, I will document my unintended solution for GPN CTF 2025’s rev/variants.

variants - 478 pts (2 solves)

A true cosmopolitan should speak many languages. And I do… but everywhere I go, people seem to understand different things…

Could you help me find a consensus they can all agree on? Someone might even give you a flag for it.

Unintended Solution

Crypto in a Rev Challenge?

If we open up the binary in Binary Ninja and click around for a bit, we can see the following data:

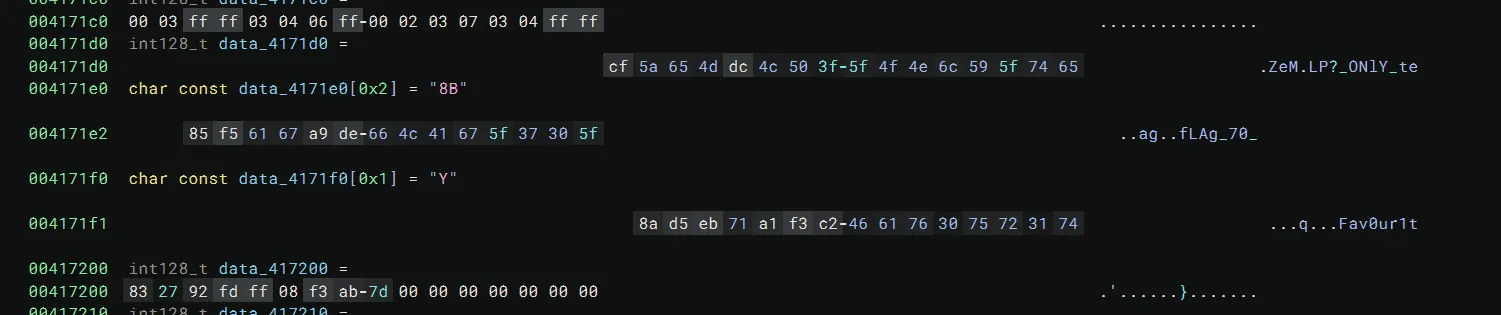
It appears to be the flag, but mangled somehow.

Binary Ninja tells us that this mangled flag data is referenced by the following function:

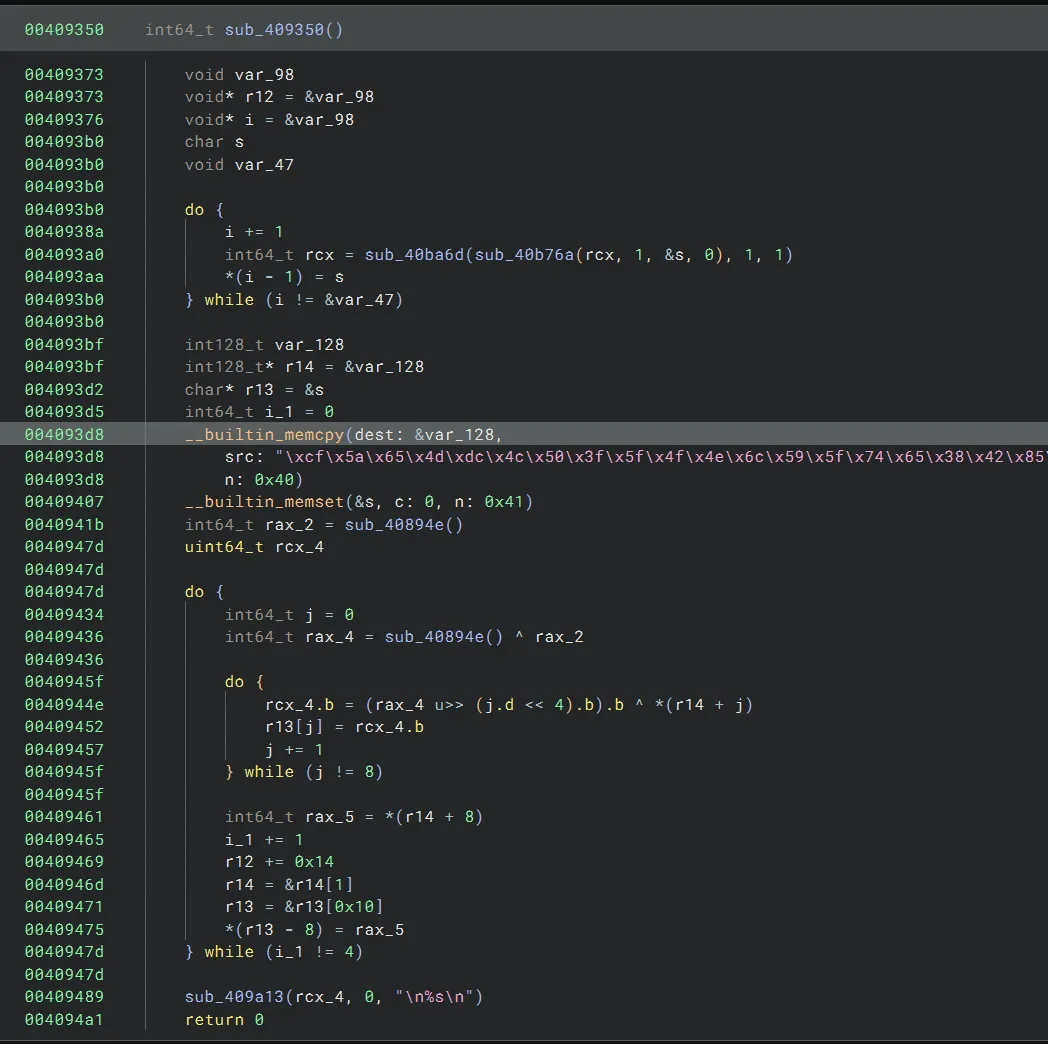
This function appears to implement some sort of XOR cipher, where the flag is broken up into chunks of 8 bytes. Every other chunk of 8 bytes is decrypted with some unique XOR key to get the flag (I refer to these chunks as “mangled” chunks). The remaining chunks that are not mangled are just in plaintext. Here, I’ve reassigned some names and types to make the decompilation cleaner:

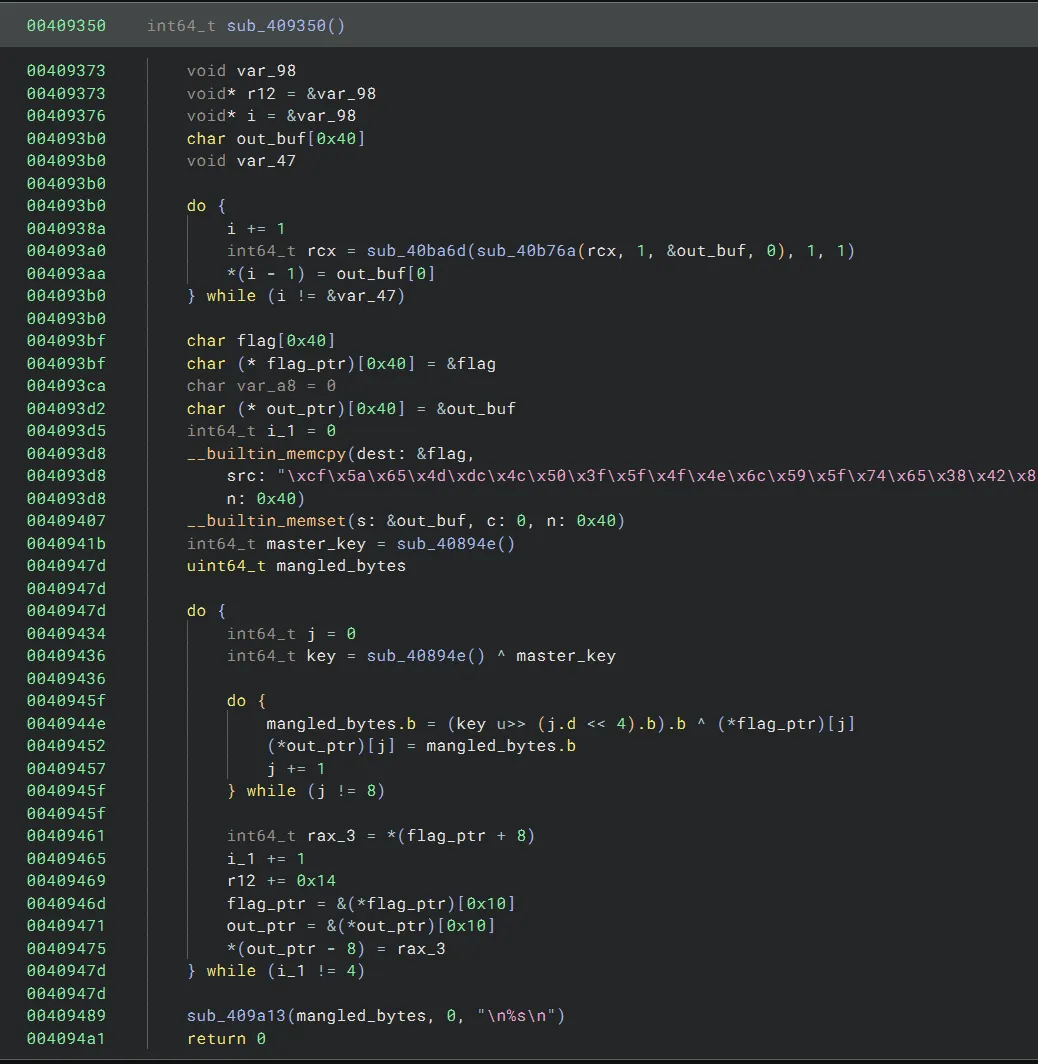
Take a look at the loop here that steps through each byte of a mangled chunk, and XOR decrypts the mangled byte:

The byte chosen as the XOR key for each mangled byte is (key >> (j << 4)) & 0xff. Notice that j ranges from 0 to 7 and key is right-shifted by j << 4. Here’s a table of j-values and their associated key shifts:

1
j = 0    ->    j << 4 = 0      ->    (key >> 0) & 0xff
2
j = 1    ->    j << 4 = 16     ->    (key >> 16) & 0xff
3
j = 2    ->    j << 4 = 32     ->    (key >> 32) & 0xff
4
j = 3    ->    j << 4 = 48     ->    (key >> 48) & 0xff
5
j = 4    ->    j << 4 = 64     ->    (key >> 64) & 0xff
6
j = 5    ->    j << 4 = 80     ->    (key >> 80) & 0xff
7
j = 6    ->    j << 4 = 96     ->    (key >> 96) & 0xff
8
j = 7    ->    j << 4 = 112    ->    (key >> 112) & 0xff

Notice that key is only a 64-bit variable though… So, what happens if a 64-bit variable is shifted by a shift that is greater than 64?

A weird quirk of the x86-64 architecture is that if we are shifting a 64-bit value, say x >> N, then the shift that the CPU actually performs is x >> (N % 64). This design choice of the architecture dates all the way back to the late 1970s, where Intel used it as an optimization technique when adding variable-shift instructions to their 16-bit 8086 CPU.

What this means for us, though, is that bytes 0-3 and bytes 4-7 are XORed by the same XOR key. To see why this is true, here’s the same table as before, but accounting for the % 64 in the key shift:

1
j = 0    ->    j << 4 = 0      ->    (key >> 0) & 0xff
2
j = 1    ->    j << 4 = 16     ->    (key >> 16) & 0xff
3
j = 2    ->    j << 4 = 32     ->    (key >> 32) & 0xff
4
j = 3    ->    j << 4 = 48     ->    (key >> 48) & 0xff
5
j = 4    ->    j << 4 = 64     ->    (key >> 0) & 0xff
6
j = 5    ->    j << 4 = 80     ->    (key >> 16) & 0xff
7
j = 6    ->    j << 4 = 96     ->    (key >> 32) & 0xff
8
j = 7    ->    j << 4 = 112    ->    (key >> 48) & 0xff

Because bytes 0-3 and bytes 4-7 are XORed by the same key, we now have a mathematical relationship between these two groups of 4 bytes. From here, guessing the flag becomes a viable strategy.

Guessing the Flag

I wrote a small Python CLI program to help me with guessing the flag:

1
import string
2

3
flag = b'\xcfZeM\xdcLP?_ONlY_te8B\x85\xf5ag\xa9\xdefLAg_70_Y\x8a\xd5\xebq\xa1\xf3\xc2Fav0ur1t\x83\'\x92\xfd\xff\x08\xf3\xab}\x00\x00\x00\x00\x00\x00\x00'
4
chunks = [flag[i:i+8] for i in range(0, len(flag), 8)]
5

6
known = [
7
    (0, 0, 'G'),
8
    (0, 1, 'P'),
9
    (0, 2, 'N'),
10
    (0, 3, 'C'),
11
]
12
for i, j, c in known:
13
    index = i * 8 + j
14
    key = ord(c) ^ flag[index]
15
    chunk = bytearray(chunks[i])
16
    chunk[j] = ord(c)
17
    chunk[(j + 4) % 8] = chunks[i][(j + 4) % 8] ^ key
18
    chunks[i] = bytes(chunk)
19

20
charset = string.ascii_letters + string.digits + string.punctuation + ' '
21

22
while True:
23
    for i, chunk in enumerate(chunks):
24
        print(f'Chunk {i}:  {chunk.hex()}  {chunk}')
25

26
    chunk_index = int(input('> ').strip())
27
    if chunk_index % 2 != 0:
28
        print('Chunk is not mangled')
29
        continue
30

31
    index = int(input('char index: ').strip())
32
    other_index = (index + 4) % 8
33

34
    chunk = chunks[chunk_index]
35
    print()
36
    print(f'Chunk {i}:  {chunk.hex()}  {chunk}')
37
    print(' ' * len(f'Chunk {i}:  ') + '  ' * (min(index, other_index)) + '^^' + '  ' * 4 + '^^')
38

39
    print('possibilities:')
40
    for char in charset:
41
        key = ord(char) ^ chunk[index]
42
        if chr(chunk[other_index] ^ key) not in charset:
43
            continue
44

45
        new_chunk = bytearray(chunk)
46
        new_chunk[index] = ord(char)
47
        new_chunk[other_index] = chunk[other_index] ^ key
48
        print(f'    {char} -> {new_chunk.hex()}  {new_chunk}')
49

50
    new_char = input('new char: ').strip()
51
    key = ord(new_char) ^ chunk[index]
52
    new_chunk = bytearray(chunk)
53
    new_chunk[index] = ord(new_char)
54
    new_chunk[other_index] = chunk[other_index] ^ key
55
    chunks[chunk_index] = bytes(new_chunk)
56
    print()

This Python program automates the process of using one mangled byte to compute its other mathematically-related byte.

With a bit of guesswork, we can use this program to figure out that the flag is one of the following:

1
GPNCTF{1_ONlY_te1l_thIs_fLAg_70_my_vERy_Fav0ur1t3_PeOp13}
2
GPNCTF{1_ONlY_te1l_thIs_fLAg_70_mY_vEry_Fav0ur1t3_PeOp13}
3
GPNCTF{1_ONlY_te1l_thIs_fLAg_70_My_veRy_Fav0ur1t3_PeOp13}
4
GPNCTF{1_ONlY_te1l_thIs_fLAg_70_MY_very_Fav0ur1t3_PeOp13}
5
GPNCTF{1_ONlY_te1L_this_fLAg_70_my_vERy_Fav0ur1t3_PeOp13}
6
GPNCTF{1_ONlY_te1L_this_fLAg_70_mY_vEry_Fav0ur1t3_PeOp13}
7
GPNCTF{1_ONlY_te1L_this_fLAg_70_My_veRy_Fav0ur1t3_PeOp13}
8
GPNCTF{1_ONlY_te1L_this_fLAg_70_MY_very_Fav0ur1t3_PeOp13}

Because of the properties of ASCII, we cannot actually deduce the case for 3 of the mathematically-related pairs of flag characters. However, there are only 8 possibilities for the flag here, so we can just try submitting all of them…

GPNCTF{1_ONlY_te1l_thIs_fLAg_70_My_veRy_Fav0ur1t3_PeOp13}

Intended Solution

The binary actually implemented some form of a variant of Sudoku that used the APE Loader to split parts of the game logic into different variants of the program that run on different machines.

The intended solution was to dump all of these variants of the program, reverse engineer the rules of the Sudoku variant, then solve the puzzle.