TJCTF 2025: "golf-hardester"

Hello!

This past weekend, I played in TJCTF with les amateurs. We ended up in 1st place!

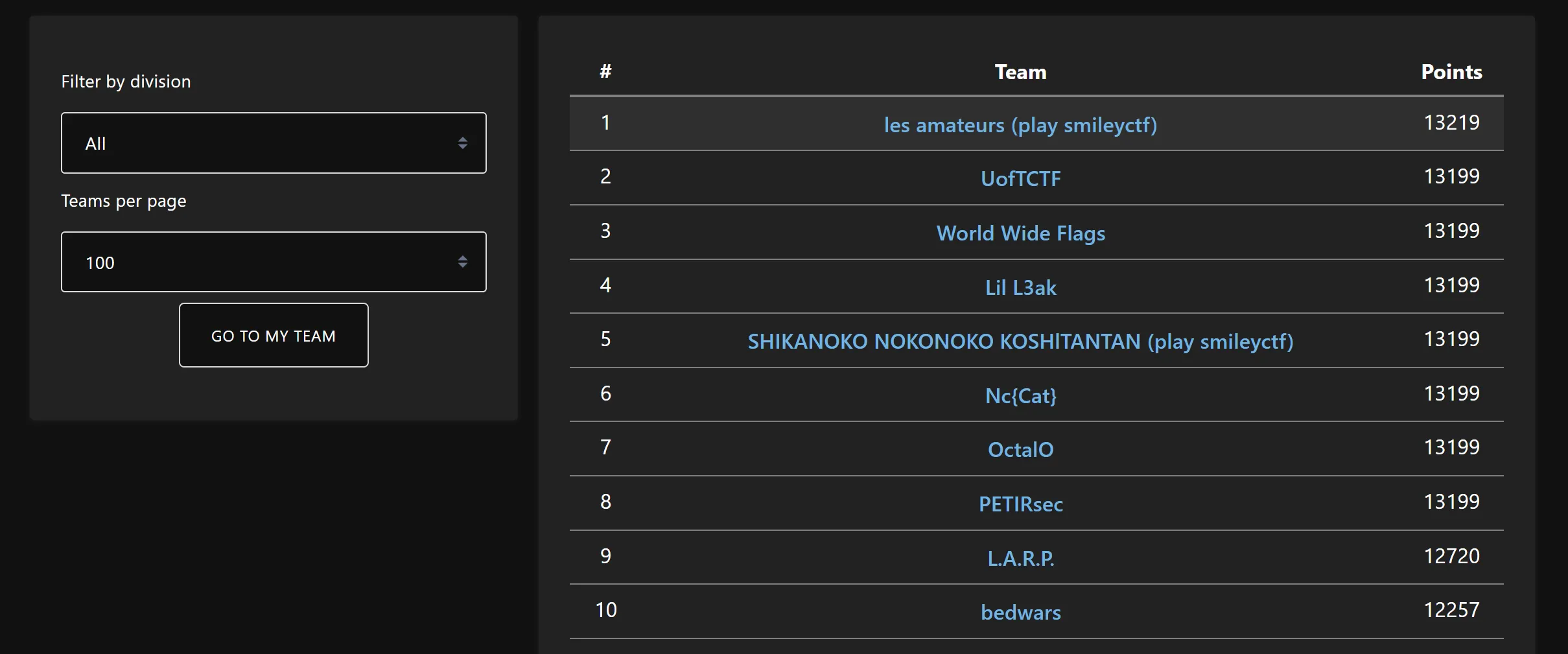
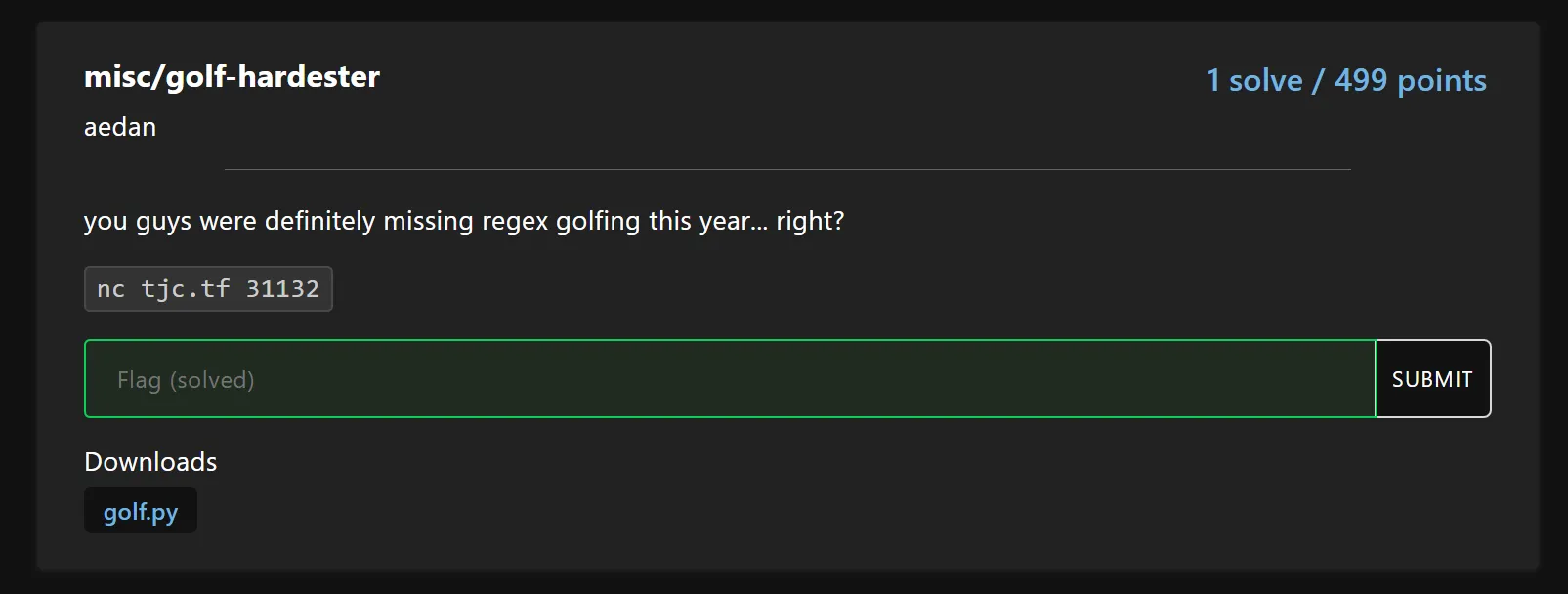
We won because we were the only team to solve misc/golf-hardester. In this write-up, I will be documenting my thought process while solving golf-hardester.

Challenge Breakdown

golf-hardester is a regex golfing challenge where you are given sample texts to match and sample texts to not match, and you must write a regex within a certain character limit that matches the pattern. There are 5 levels, each of which has its own pattern that you must write a regex for. To get the flag, you must solve all 5 levels.

In this write-up, I will mainly be focusing on level 5, as it was by far the most difficult and was the one where most teams got stuck on.

Levels 1-4

Level 1

1
1. "Warmup"
2
    This one's pretty straightforward.
3

4
Match on all of these:    But none of these:
5
------------------------  ------------------------
6
ampasimenite              jasmone
7
anchorable                decisivenesses
8
aconic                    backoff
9
antistrophic              whitebark
10
abrade                    physogastrism
11
arroya                    shavee
12
apoplex                   hanoverian
13
ayahs                     weatherstripped
14
arock                     naturalize
15
anconoid                  lophotrichous
16
anglophile                nonprecedential
17
acalephan                 tjctf
18
amaze                     shepherdia
19
adelphe                   waymark
20
anno                      picnicker
21
amiable                   bottleholder
22
aliquid                   porule
23
achromatin                diagraming
24
aircheck                  solifuge
25
antigenically             phrenetically
26

27
Maximum allowable length is 2

The pattern is just to match any string that begins with an a.

1
^a

Level 2

1
2. "Tenet"
2
    It's a classic chicken-and-egg question:
3
    Which came first, the Roman graffiti or the Christopher Nolan movie?
4

5
Match on all of these:     But none of these:
6
-------------------------  ---------------------------------------------
7
satorarepotenetoperarotas  chirl
8
decaleminacivicanimelaced  kayak
9
strawtrelareferalertwarts  croisstrutannotdawes
10
hakamanasakayakasanamakah  khnabadalanamanaladabanhk
11
dimitinarimadamiranitimid  parssalertrevertrelassrap
12
faradaromarotoramoradaraf  makahadelykerekyledahakam
13
banakaholanoyonalohakanab  crimpgruftgowermairsjessi
14
lassoartusstetssutraossal  nasabbnamasamasamanbbasan
15
rakisanolikodokilonasikar  mfssaartusstatssutraassfm
16
tadesaneledewedelenasedat  camusvmelumesemulemvsumac
17
assetscamesalasemacstessa  tknakaronanoyonanorakankt
18
cestiecartsamastraceitsec  sejabenemarexeramenebajes
19
gnatsnonetananatenonstang  esshmshamasamasamahsmhsse
20
rotasoperatevetareposator  talasaladalwvwladalasalat
21
rakesamenekeyekenemasekar  talasadelslemelsledasalat
22
salemanelelemelelenamelas  areposatortenetrotasopera
23
assesspalesamaselapssessa  faradaledaaeveaadeladaraf
24
dartsavertrevertrevastrad  assamshampsalaspmahsmassa
25
coramoletareveratelomaroc  nesoaevilssirissliveaosen
26
nertaecartradartraceatren  zaiananasamadamasananaiaz
27
haramadelareferaledamarah  kayakkayakkayakkayakkayak
28
latonanimotipitominanotal  kanltadalanamanaladatlnak
29
kedarenemadewedameneradek  batheskaldifritfacksladesremop
30
masseattisstatssittaessam  awhetmeresfatalabdulaboonamulagiamo
31
kelsielapslavalspaleislek  ervumkemmemuzakalgiaapersdikesswinkrizzo
32
waresalonerotorenolaseraw  avenspairtstrohaddiasixthaeriesclavtepeecribs
33
susanulemasexesamelunasus
34

35
Maximum allowable length is 50

The pattern here is a bit difficult to see, but the rule is to match any string that matches the following conditions:

1. The string must be a palindrome.
2. The string must be 25 characters long.
3. The 2nd character must be the same as the 6th character.
4. The 3rd character must be the same as the 11th character.
5. The 4th character must be the same as the 10th character.
6. The 7th character must be the same as the 12th character.

To match a palindrome, we can use the regex module’s recursion feature. This regex matches any palindrome:

1
^(.|(.)(?1)\2)$

Here, we have a base case of a single character. In the recursive case, we capture a character, recursively match the regex, then backreference the captured character to ensure it occurs again at the end of the string.

We can match conditions 2-6 with the following regex:

1
^.(.)(.)(.).\1.(.).\3\2\4.{13}$

We can then combine the two regexes using a lookahead:

1
^(?=(.|(.)(?1)\2)$).(.)(.)(.).\3.(.).\5\4\6.{13}$

Level 3

1
3. "Triumvirate"
2
    Ah yes, quinary, my fifth favorite base.
3

4
Match on all of these:               But none of these:
5
-----------------------------------  ----------------------------------
6
0                                    1
7
3                                    4
8
11                                   210
9
14                                   11310
10
22                                   214131244
11
30                                   3213002030
12
2402301                              303032014212
13
2423144312                           231332302134
14
111413130043                         110220031020430
15
3402023233320                        1422343112104210
16
130424322431012                      110310304112132043
17
31243200410022310                    100210421022044210
18
1420210414114303030                  1114412243313242103
19
302100312023023123                   24440314200314423044
20
2020212213114432333240               10431021421031033200
21
1243332123330120041301               43114042320203440411
22
1403212440313014044442               1122103140022040312224
23
32301404334330404131321              20113122400131413033301
24
413011141021024302200400             114042013123013231123102344
25
4210332323242404120224132            102310311320124044204140131
26
114401022024420003234234444          1000441233101220230414004112333
27
13020411424304401310144130040302     10212311344141143012420443230301
28
11202241201424204222113011221133     20121332123142340324001223212344
29
234343341022001132401403022101104    42441333222430014043301433413001
30
231421441204321403132040024202002    242310103234324100011331130230334
31
10410400231012014340122214134013042  1441413341001141224132000024031214
32

33
Maximum allowable length is 70

The pattern here is to match any base-5 number that is divisible by 3.

The idea here is that we will step through each digit, and keep a running count of the number modulo 3. Once we reach the end of the string, our running count will be the entire number, modulo 3. Thus, we can match only strings that end with a running count of 0 (mod 3). For example, consider the base-5 number 124 (39 in decimal). This is how our regex will evaluate it:

1
count starts at 0
2
[1]23 -> count = (count * 5) + 1 = (0 * 5) + 1 = 1 (mod 3)
3
1[2]3 -> count = (count * 5) + 2 = (1 * 5) + 2 = 1 (mod 3)
4
12[4] -> count = (count * 5) + 4 = (1 * 5) + 4 = 0 (mod 3)
5
string ends with count = 0, so we accept it

The trick here is that, because we are operating mod 3, the count variable can only have 3 values: 0, 1, or 2. We can create three separate regexes to model each possible value of count:

1
count_0: $|[03](?&count_0)|[14](?&count_1)|2(?&count_2)
2
count_1: [03](?&count_2)|[14](?&count_0)|2(?&count_1)
3
count_2: [03](?&count_1)|[14](?&count_2)|2(?&count_0)

Combining these three regexes, and stripping group names to make it shorter, we get:

1
^($|[03](?1)|[14]([03]([03](?2)|[14](?3)|2(?1))|[14](?1)|2(?2))|2(?3))

Level 4

1
4. "Lucky Number"
2
    I don't think you need any hints as to which base this is.
3

4
Match on all of these:    But none of these:
5
------------------------  ------------------------
6
0                         1
7
111                       10
8
1110                      11
9
10101                     100
10
11100                     101
11
100011                    110
12
101010                    1000
13
110001                    1001
14
111000                    1010
15
111111                    1011
16
1000110                   1100
17
1001101                   1101
18
1010100                   1111
19
1011011                   10000
20
1100010                   10001
21
1101001                   10010
22
1110000                   10011
23
1110111                   10100
24
1111110                   10110
25
10000101                  10111
26
10001100                  101101
27
10010011                  1100001
28
10011010                  1101111
29
10100001                  10111011
30
10101000                  11110100
31
10101111                  11110111
32
10110110                  100110110
33
10111101                  100001111
34
11000100                  110001010
35
11001011                  111110000
36
11010010                  101101001
37
11011001                  110111110
38
11100000                  1011100011
39
11100111                  1010010111
40
11101110                  1110000001
41
11110101                  1011011011
42
11111100                  1001101110
43
100000011                 1011110110
44
100001010                 1001100110
45
100010001                 1010001111
46

47
Maximum allowable length is 162

The pattern here is to match any base-2 number that is divisible by 7.

We can use the same technique as in level 3.

1
^(?<s0>$|0(?&s0)|1(?<s1>0(?<s2>0(?<s4>0(?&s1)|1(?&s2))|1(?<s5>0(?&s3)|1(?&s4)))|1(?<s3>0(?<s6>0(?&s5)|1(?&s6))|1(?&s0))))

Level 5

1
5. "Tally"
2
    Alright, time for a real challenge. This one should actually be difficult!
3

4
Match on all of these:    But none of these:
5
------------------------  ------------------------
6
arraigning                edified
7
nonordered                unreverberating
8
abadbacdcacbdbdc          underpass
9
mesosome                  interinsert
10
ananna                    pilfered
11
unendued                  nippiness
12
tromometer                gregarinian
13
caucasus                  deicide
14
intestines                nonaristocratic
15
i                         rototiller
16
deed                      ozonizing
17
horseshoer                museums
18
happenchance              backbreaker
19
reappear                  interradiated
20
deeded                    antistalling
21
pullup                    naturalize
22
arraigning                equitriangular
23
testes                    reparticipate
24
mononymy                  ppd
25
scintillescent            miasmas
26
couscous                  cabbage
27

28
Maximum allowable length is 62

Now, we get to the last level, and the hardest one by far.

Luckily, by the time that I had gotten to this level, the author had already released a hint about what the pattern to match is:

We need to match any string that has equal number of occurrences of all the unique characters in the string.

Brainstorming

One of the first things that my teammate and I noticed was that because of the transitive property of equality, we only actually need to check that a given character has the same number of occurrences as only one other character in the string. We do not need to test every character against every other character.

For example, in the string aabbcc:

1. Checking a against b, they both have 2 occurrences.
2. Checking b against c, they both have 2 occurrences.
3. We automatically know that a and c have the same number of occurrences by the transitive property of equality.

This insight allows us to come up with an algorithm that may be possible to implement in regex that satisfies the pattern:

1. Step through each character in the string.
2. Check if the current character and the character that follows it have the same number of occurrences.
3. If all characters pass this test, then the string is valid.

Now that we had an idea for an algorithm, I started implementing it in regex. My goal was to first implement a regex that passes the test cases, then to golf it down to fit into the 62 character limit.

Matching Equal Counts (part 1)

Starting simply, I first wanted to make a regex that matched any string that had equal counts of the characters a and b, assuming the string had no other characters other than as and bs.

The key insight that I had here is: if there are equal counts of as and bs, then we can pair up every single a with a single b. Thus, if the first character is an a, then there must be a b somewhere later in the string that we can pair the a up with (and vice versa).

In regex, that would look something like this:

1
^(a.*b|b.*a)

It is possible for there to be multiple pairs of as and bs in the string. For example, consider the string abba. This string has two pairs: ab and ba. So, we need to repeat this pairing pattern until the end:

1
^(a.*b|b.*a)*$

Up until now, we have been ignoring the portion of the string between the paired a and b characters with a .*. However, we also need to ensure that this substring has an equal number of as and bs. For example, consider the string aabb. This string contains an ab pair within an ab pair. This is a perfect use case for recursion! So, our new regex looks like this:

1
^(a(?1)*b|b(?1)*a)*$

This regex matches any string with an equal count of as and bs, assuming the string only contains as and bs.

Matching Equal Counts (part 2)

Now, we can extend this regex to match any string with equal counts of as and bs, regardless of what other characters it contains.

All that we need to do this is to skip characters that are not as or bs. One way we could do this is with an exclusive set. In regex, the set [^ab] will match any character that is not an a or b. So, we can modify our regex as such:

1
^([^ab]+|a(?1)*b|b(?1)*a)*$

However, eventually, we will want to use this regex to test any arbitrary captured characters, not just a and b. Unfortunately, we cannot put backreferenced captured strings into a set, so we will need to use a different approach to match any character except a or b.

The method I came up with to do this is using negative lookaheads. Putting a negative lookahead before a pattern will cause that pattern to not match if the negative lookahead matches. So, the following pattern will match any character that is not an a or b:

1
(?!a|b).

We can replace our exclusive set with this negative lookahead:

1
^(((?!a|b).)+|a(?1)*b|b(?1)*a)*$

We now have a regex that matches any string with equal counts of as and bs, while ignoring all other characters!

Extending to Captured Characters

Now, we can extend our regex to match any two characters, not just a and b. Our original algorithm idea was to step through the string and check if consecutive characters have equal counts. For now, we will not worry about stepping through the string; we will only check if the first character has the same count as the second character.

To start, we just need to capture the first and second characters:

1
^(.)(.)

However, we run into an issue here. We can’t just append our equal-counts regex after the captures because the captures have already consumed the first two characters of the string. Our equal-counts regex must run on the entire string.

Furthermore, our equal-counts regex must not consume any characters; eventually, we will have to extend this regex to step through the string character-by-character. The only way to iterate through the string is to consume characters one-by-one, so if the equal-counts regex consumed characters, it would disturb the iteration.

The solution I came up with is to first use a positive lookahead to go to the end of the string, then use a negative lookahead to reset the position back to the start of the string. Lookaheads do not consume characters, so this does exactly what we need! This technique looks like this:

1
(?=
2
    .*$     # Goto end of string
3
    (?<=
4
        ^   # Reset back to beginning of string
5

6
        # Equal-counts regex:
7
        (((?!a|b).)+|a(?1)*b|b(?1)*a)*$
8
    )
9
)

Now, we can append this to the regex that captures the first and second characters, and substitute the equal-counts regex’s a and b with group backreferences:

1
^(.)(.)
2
(?=
3
    .*$     # Goto end of string
4
    (?<=
5
        ^   # Reset back to beginning of string
6

7
        # Equal-counts regex:
8
        (((?!\1|\2).)+|\1(?3)*\2|\2(?3)*\1)*$
9
    )
10
)

Great! We now have a regex that matches any string with equal counts of the first two characters.

Iterating the String

Our original algorithm idea was to iterate through the string and check if consecutive characters have equal counts. I did spend about an hour trying to implement this, and came up with the following regex:

1
^
2
(?:(.)(?=$|(.)
3

4
.*$(?<=^
5

6
    (?<main_loop>
7
    ((?!\1|\2).)+
8
    |\1(?&main_loop)*\2
9
    |\2(?&main_loop)*\1
10
    )*
11

12
$)
13

14
))*
15
$

It did seem to work somewhat well (passed all but a few testcases), but it felt very clunky, inefficient, and used up an unnecessary amount of characters. The main issues with checking if consecutive characters have equal counts were:

1. The last character in the string is an edge case that needs special handling, as it has no character after it to compare against. This adds complexity and uses up characters.
2. To compare the current character with the character after it, we have to somehow capture the character after the current character without consuming it; I accomplished this by putting a capture in a lookahead, but, this seemed to cause weird, buggy behavior in the regex engine (more on that later).

While working on this regex, I realized that a much more regex-friendly algorithm would be to just capture the first character and compare the counts of every other character against it; rather than comparing the counts of consecutive characters. This algorithm still works due to the aforementioned transitive property of equality.

This new approach eliminates both of the issues with the previous regex:

1
^
2
# Capture first character; we will test everything against it
3
(.)
4

5
(?:
6
# Capture next character to test against the first
7
(.)
8

9
    (?=
10
    # Goto end of string
11
    .*$
12
        (?<=
13

14
        # Test if chars in \1 and \2 have same counts in the string
15
        ^
16
        (?<main_loop>
17
        ((?!\1|\2).)+  # skip
18
        |\1(?&main_loop)*\2
19
        |\2(?&main_loop)*\1
20
        )*
21
        $
22

23
        )
24
    )
25

26
)*
27
$

We’re almost there! This regex passes every test case, except for three. This regex fails to match the following strings:

1
annana
2
deeded
3
pullup

Eliminating an Edge Case

Determining the issue with annana and deeded was not too difficult.

Consider the case of annana. The issue here is that as the regex iterates the string, it will eventually try to check if a has the same count as a. When phrased in English, this sounds like it should pass. However, recall how our equal-counts regex works: in this case, it will try to pair up every single a with another a. This fails in the case of annana because there are an odd number of as in the string, so the regex cannot pair up every a with another a.

The issue is identical for deeded, as there is an odd number of ds.

The solution here is simple: we just need to skip checking if a character has the same count as itself. We can do this by adding a special case for this scenario:

1
^
2
# Capture first character; we will test everything against it
3
(.)
4

5
(?:
6
\1|  # Skip matching a character against itself
7

8
# Capture next character to test against the first
9
(.)
10

11
    (?=
12
    # Goto end of string
13
    .*$
14
        (?<=
15

16
        # Test if chars in \1 and \2 have same counts in the string
17
        ^
18
        (?<main_loop>
19
        ((?!\1|\2).)+  # skip
20
        |\1(?&main_loop)*\2
21
        |\2(?&main_loop)*\1
22
        )*
23
        $
24

25
        )
26
    )
27

28
)*
29
$

Now, our regex passes all test cases but one: pullup.

Fighting with the Regex Engine (part 1)

This is where things start to get weird.

It’s not immediately obvious why pullup fails. Stranger still, if I change the quantifier on the string iteration loop (line 28) from * to a +?, then suddenly pullup passes, but reappear fails.

What?

That quantifier should have no effect here; the only difference between * and +? is that * is greedy (will try to match as much as possible) while +? is lazy (will try to match as little as possible). However, we immediately follow up the quantifier with an end-of-string anchor ($), so whether it is greedy or lazy should not affect the match at all.

This is where I started to suspect a bug in the regex module. Seeing as how the slightest, seemingly inconsequential change to the regex caused differing results, I decided that if I just randomly messed around with the regex enough, then maybe I could stumble across a way to make the regex engine not bug out, and pass all test cases.

Indeed, eventually I found that if I use a recursive loop to iterate over the string rather than a * quantifier, then we do pass all the test cases!

1
^
2
# Capture first character; we will test everything against it
3
(?<a>.)
4

5
(?<big_loop>
6
$|
7

8
\g<a>(?&big_loop)|  # Skip matching a character against itself
9

10
# Capture next character to test against the first
11
(?<b>.)
12

13
    (?=
14
    # Goto end of string
15
    .*$
16
        (?<=
17

18
        # Test if chars in \g<a> and \g<b> have same counts in the string
19
        ^
20
        (?<main_loop>
21
        ((?!\g<a>|\g<b>).)+  # skip
22
        |\g<a>(?&main_loop)*\g<b>
23
        |\g<b>(?&main_loop)*\g<a>
24
        )*
25
        $
26

27
        )
28
    )
29

30
(?2)
31
)

Cutting Characters

We now have a regex that passes all test cases, but unfortunately, when minified, it is 72 characters long (reminder, we need it to be 62 characters or less):

1
^(.)($|\1(?2)|(.)(?=.*$(?<=^(((?!\1|\3).)+|\1(?4)*\3|\3(?4)*\1)*$))(?2))

The first change I came up with to cut characters was in the equal-counts regex: it is unnecessary to put a repeating quantifier on the skipping-character case, (?!\1|\2)., as all uses of main_loop already have a repeating quantifier. This saves 3 characters, and looks as follows:

1
^
2
(?<main_loop>
3
 ((?!\1|\2).)+  # skip
4
 (?!\1|\2).  # skip
5
|\1(?&main_loop)*\2
6
|\2(?&main_loop)*\1
7
)*
8
$

Furthermore, we can remove the $ after the equal-counts regex. This is because the equal-counts regex is contained within a lookbehind that occurs at the end of the string, so the equal-counts regex must necessarily match until the end of the string. This saves another character:

1
# Goto end of string
2
.*$
3
    (?<=
4

5
    # Test if chars in \g<a> and \g<b> have same counts in the string
6
    ^
7
    (?<main_loop>
8
    ((?!\g<a>|\g<b>).)+  # skip
9
    |\g<a>(?&main_loop)*\g<b>
10
    |\g<b>(?&main_loop)*\g<a>
11
    )*
12
    $
13

14
    )
15
)

We are now down to 68 characters:

1
^(.)($|\1(?2)|(.)(?=.*$(?<=^((?!\1|\3).|\1(?4)*\3|\3(?4)*\1)*))(?2))

If only we could replace this clunky, hacky recursive string iteration loop with a simple, concise non-recursive loop…

Fighting with the Regex Engine (part 2)

At this point, I just started noodling around with the regex, trying to find a way to use a non-recursive loop to iterate over the string while having the regex module not bug out.

After some time, I discovered that, while (...)* and (...)+? may not have worked to iterate over the string, ((...)+)? did.

…

This brought the regex down to 63 characters:

1
^(.)((\1|(.)(?=.*$(?<=^((?!\1|\4).|\1(?5)*\4|\4(?5)*\1)*)))+)?$

Unminified, the regex looked as follows:

1
# Capture first character; we will test everything against it
2
^
3
(?<a>.)
4

5
((
6
    \g<a>|  # Skip matching a character against itself
7

8
    # Capture next character to test against the first
9
    (?<b>.)
10
    (?=
11
    # Goto end of string
12
    .*$
13
        (?<=
14

15
        # Test if chars in \g<a> and \g<b> have same counts in the string
16
        ^
17
        (?<main_loop>
18
            (?!\g<a>|\g<b>).  # skip
19
            |\g<a>(?&main_loop)*\g<b>
20
            |\g<b>(?&main_loop)*\g<a>
21
        )*
22

23
        )
24
    )
25
)+)?$

After some more noodling around, I discovered that the following changes to the regex cuts it down to exactly 62 characters (minified) and is able to pass all test cases:

1
# Capture first character; we will test everything against it
2
^
3
(?<a>.)
4

5
 ((
6
 (
7
    \g<a>|  # Skip matching a character against itself
8

9
    # Capture next character to test against the first
10
    (?<b>.)
11
    (?=
12
    # Goto end of string
13
    .*$
14
        (?<=
15

16
        # Test if chars in \g<a> and \g<b> have same counts in the string
17
        ^
18
        (?<main_loop>
19
            (?!\g<a>|\g<b>).  # skip
20
            |\g<a>(?&main_loop)*\g<b>
21
            |\g<b>(?&main_loop)*\g<a>
22
            |\g<a>(?&main_loop)*?\g<b>
23
            |\g<b>(?&main_loop)*?\g<a>
24
        )*
25

26
        )
27
    )
28
 )+)?$
29
 )*$

Minified:

1
^(.)(\1|(.)(?=.*$(?<=^((?!\1|\3).|\1(?4)*?\3|\3(?4)*?\1)*)))*$

I honestly have no clue why this worked.

tjctf{davidebyzero_is_my_hero_6a452cbdc75f}

Solve Scripts

Final regex:

1
^(.)(\1|(.)(?=.*$(?<=^((?!\1|\3).|\1(?4)*?\3|\3(?4)*?\1)*)))*$

Annotated:

1
# Want to check if the string has equal counts of all the unique characters
2

3
# Capture first character; we will test everything against it
4
^
5
(?<a>.)
6

7
(
8
    \g<a>|  # Skip matching a character against itself
9

10
    # Capture next character to test against the first
11
    (?<b>.)
12
    (?=
13
    # Goto end of string
14
    .*$
15
        (?<=
16

17
        # Test if chars in \g<a> and \g<b> have same counts in the string
18
        ^
19
        (?<main_loop>
20
            (?!\g<a>|\g<b>).  # skip
21
            |\g<a>(?&main_loop)*?\g<b>
22
            |\g<b>(?&main_loop)*?\g<a>
23
        )*
24

25
        )
26
    )
27
)*$

1
import pwn
2

3
r = pwn.remote('tjc.tf', 31132)
4
r.sendlineafter(b'> ', br'^a')
5
r.sendlineafter(b'> ', br'^(?=(.|(.)(?1)\2)$).(.)(.)(.).\3.(.).\5\4\6.{13}$')
6
r.sendlineafter(b'> ', br'^($|[03](?1)|[14]([03]([03](?2)|[14](?3)|2(?1))|[14](?1)|2(?2))|2(?3))')
7
r.sendlineafter(b'> ', br'^(?<s0>$|0(?&s0)|1(?<s1>0(?<s2>0(?<s4>0(?&s1)|1(?&s2))|1(?<s5>0(?&s3)|1(?&s4)))|1(?<s3>0(?<s6>0(?&s5)|1(?&s6))|1(?&s0))))')
8
r.sendlineafter(b'> ', br'^(.)(\1|(.)(?=.*$(?<=^((?!\1|\3).|\1(?4)*?\3|\3(?4)*?\1)*)))*$')
9
r.interactive()

So… what was up with the regex engine?

After the CTF, the challenge author suggested that the strange regex engine behavior I was encountering likely had to do with the atomic behavior of lookarounds (it probably wasn’t a bug):